Continuando o post anterior, onde falávamos sobre o exercício proposto pelo Rodrigo Yoshima, no #LKBR19 , como podemos confiar se a previsibilidade apontada pelos cálculos é confiável?
Podemos utilizar métodos de simulação, como a Simulação de Monte Carlo. Existem diversos métodos de simulação, mas a Simulação de Monte de Carlo é bem simples e muito confiável.
Na sua forma mais simples, a Simulação de Monte Carlo pode ser pensada como um conjunto de experimentos com números aleatórios. O método é normalmente aplicado a problemas altamente incertos, onde a computação direta é difícil, impraticável ou impossível. Ele provou ser uma ferramenta útil em muitos campos, incluindo física nuclear, exploração de petróleo e gás, finanças e seguros. Dada a incerteza no trabalho do conhecimento, parece estranho que nossa indústria tenha chegado um pouco tarde à Simulação de Monte Carlo. Pode-se argumentar que foi necessário o surgimento de métodos ágeis modernos para chegar ao ponto em que podemos até modelar o trabalho que fazemos para simulação. Independentemente disso, acredito firmemente que o Método Monte Carlo é o futuro da previsão no trabalho do conhecimento.
Diante do cenário do exercício, onde trabalhamos com médias, para termos maior qualidade na simulação, teríamos que ter os dados de vazão (Throughput) realizados para podermos executar o modelo. Não tendo estes dados, faremos aqui uma simulação usando o Lead Time.
Na fórmula da Lei de Little, no exercício passado, temos um lead time médio, o histograma da distribuição e o wip estável em 8. Pois bem, com estes dados, podemos ter a média do Lead Time e o Desvio Médio da distribuição. Desta forma, é possível gerar números aleatórios para o lead time, repetidas vezes, por exemplo, 15.000 vezes. Ou um milhão de vezes. Vai depender da sua capacidade computacional disponível
No excel eu usei a fórmula INV.LOGNORMAL(probabilidade, média, desv_padrão), que retorna o inverso da função de distribuição cumulativa lognormal de x, em que ln(x) normalmente é distribuída com os parâmetros Média e Desv_padrão. Se p = DIST.LOGNORMAL.N(x,…) então INV.LOGNORMAL(p,…) = x. Para este exercício, no lugar do desvio padrão, fiz uso do desvio médio.
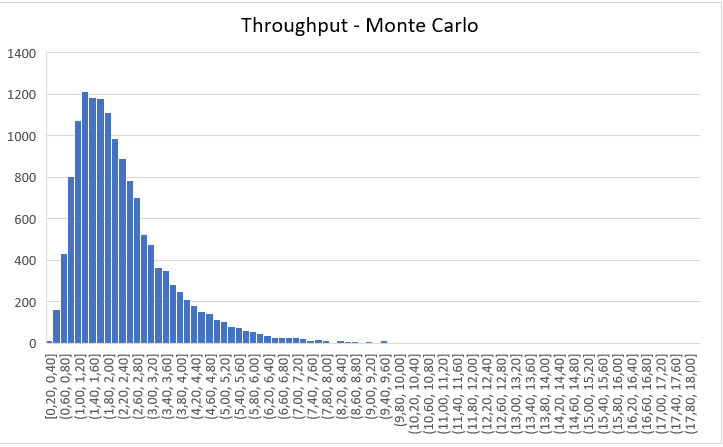
Ao fazer isto, temos este histograma da distribuição de lead time:
Com estes dados gerados, podemos também gerar dados aleatórios para o Throughput, por meio da fórmula da Lei de Little, TH = WIP/LT. Como a fórmula é uma média, geramos valores aleatórios para o Throughput aplicando um valor aleatório para a probabilidade de acontecer aquele valor de Throughput. Podemos dizer que este valor aleatório da probabilidade seja um valor do risco de acontecer aquele Throughput.
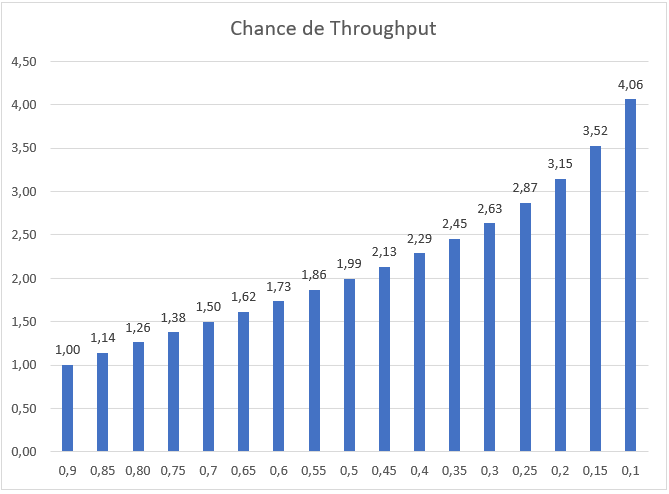
Vejamos o gráfico gerado.
Com base nos dados gerados pela simulação, podemos verificar os percentis (ou chance de um valor acontecer) da simulação gerada. Pelo gráfico, podemos perceber que temos uma chance de 10% de termos 4,06 itens entregues por dia e uma chance de 90% de termos 1,0 item entregue por dia. Os valores médios de vazão (Throughput) do exercício ficaram em 1,71 itens por dia. De acordo com o gráfico, a chance de fato acontecer novamente fica entre 60 e 65% (1,73 e 1.65 itens por dia no mínimo, respectivamente).
Reforçando, estamos lidando com médias. É um bom começo, mas não é suficiente. Precisamos lidar com probabilidade de risco ou chances do evento acontecer entre 70 e 85% de chance. E quanto mais for qualificada a amostra, melhor será a simulação.
Uma última coisa. Percebeu que os gráficos de lead time e Throughput tem uma cauda “gorda”? Qual o motivo disto? E qual o impacto?
Vamos fala disto em um próximo post !
Até mais!